
Der Goldene Schnitt: Was steckt hinter der Schönheitsformel der Natur?

Laut der deutschen Redewendung liegt die Schönheit im Auge des Betrachters. Dennoch gibt es eine Vielzahl von Beispielen, bei denen sich Menschen sofort einig sind: Sie verbinden Harmonie, Schönheit und Ästhetik. Doch ist diese Schönheit auch messbar? Ja, das ist sie und sie ist besser bekannt als der Goldene Schnitt.
Bereits die antiken Griechen benutzten dieses Maß, um natürliche Schönheit in menschliche Kreationen wie Statuen und Tempel zu bringen. Dies gelang ihnen mithilfe eines einfachen mathematischen Verhältnisses – genauer gesagt mit der Zahl 1,61803399, dargestellt durch den griechischen Buchstaben Phi (φ).
„Einige der größten mathematischen Geister aller Zeiten, von Pythagoras und Euklid im antiken Griechenland über den mittelalterlichen italienischen Mathematiker Leonardo von Pisa [nicht da Vinci] und den Astronomen Johannes Kepler bis hin zu heutigen Wissenschaftlern, haben endlose Stunden über dieses einfache Verhältnis und seine Eigenschaften nachgedacht. Doch die Faszination für den Goldenen Schnitt ist nicht nur auf Mathematiker beschränkt. Man kann wohl mit Fug und Recht behaupten, dass der Goldene Schnitt Denker aller Disziplinen inspiriert hat wie keine andere Zahl in der Geschichte der Mathematik“, schreibt der israelische Astrophysiker Mario Livio in seinem Buch „The Golden Ratio“.
Wie funktioniert der Goldene Schnitt?
Hinter dem Goldenen Schnitt versteckt sich ein ganz bestimmtes Teilungsverhältnis zweier Größen zueinander. Es ergibt sich, wenn das Verhältnis beider Größen zueinander genauso groß ist wie das Verhältnis ihrer Summe zum größeren der beiden Werte. Ausgedrückt in einer Formel heißt das: a / b = (a + b) / a.
Mit anderen Worten: Teilt man die größere Strecke (A) durch die kleinere (B), erhält man die Zahl 1,618. Dasselbe Ergebnis ergibt sich aus der Summe der beiden Strecken (A + B = C), geteilt durch die größere Strecke (A).
Deutlich anschaulicher lässt sich der Goldene Schnitt am berühmten Eiffelturm in Paris erklären: Die zweite Etage – in 116 Metern Höhe – teilt die ursprüngliche Gesamthöhe des Turms von 312 Meter (fast) im Goldenen Schnitt. Der obere Abschnitt, geteilt durch den unteren Abschnitt, ergibt das Verhältnis 1,69. Die Gesamthöhe im Verhältnis zum oberen Abschnitt ergibt 1,59. – Die erste Idee ging von einem 305 Meter hohen Turm aus, dabei hätten sich die Verhältnisse 1,61 und 1,63 ergeben.
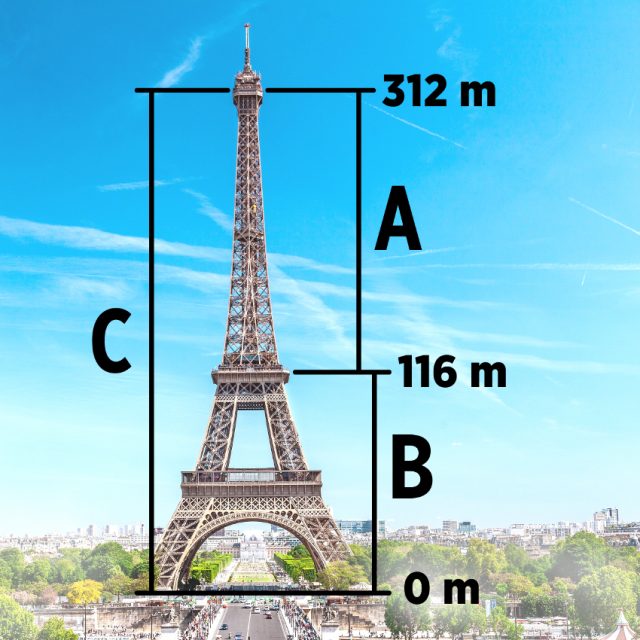
Der Eiffelturm in Paris ist fast perfekt im Goldenen Schnitt gebaut. Foto: iStock / Epoch Times
Dieses Verhältnis findet sich zudem in der Fibonacci-Folge (1, 2, 3, 5, 8, 13, …) des italienischen Mathematikers Leonardo da Pisa wider. Jede Zahl aus der Reihe ergibt sich aus der Summe der beiden vorhergehenden Zahlen. Umso größer die Summe wird, desto näher kommt das Verhältnis zweier aufeinanderfolgender Zahlen (2:3, 3:5, 5:8) dem Goldenen Schnitt. Überträgt man die Fibonacci-Folge auf eine Fläche, entsteht die typische regelmäßige Spirale – wie sie in der Natur bei Schnecken und dem Nautilus zu finden ist.
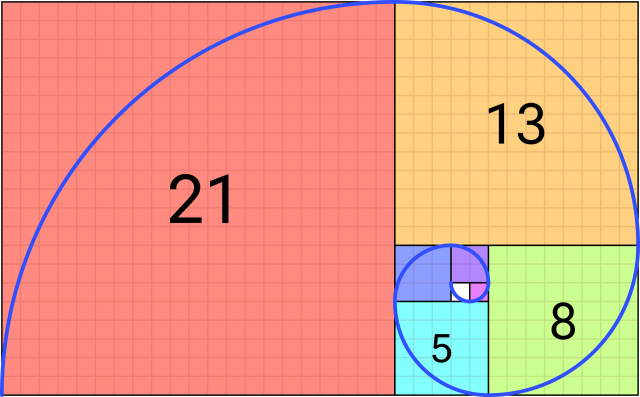
Je größer die Zahlen der Fibonacci-Folge sind, desto näher kommt ihr Verhältnis dem Goldenen Schnitt. Foto: Romain/Wikimedia Commons (CC BY-SA 4.0)
Der Goldene Schnitt beschränkt sich jedoch nicht nur auf Strecken oder Flächen. So lässt er sich zudem in beliebigen Größen darstellen, auch in Winkeln. Das Prinzip bleibt das gleiche und findet sich überaus häufig bei Blütenblättern. Ein neues Blatt entsteht dabei immer im goldenen Winkel zum vorhergehenden Blatt. Auch wenn dies auf den ersten Blick unlogisch erscheint, hat es einen praktischen Nutzen: Dank dieser Anordnung erhalten alle Blütenblätter den gleichen Anteil an Sonnenlicht.

Der goldene Winkel bei Blumen: Ein neues Blatt entsteht immer im goldenen Winkel zum vorhergehenden Blatt (siehe Nummerierung). Foto: iStock / Epoch Times
Wer hat es erfunden?
Der Erfinder der Erfolgsformel ist die Natur selbst. Welches irdische Genie verwendete den Goldenen Schnitt als Erstes in seinen Werken? Diese Frage wird noch heute viel diskutiert. Fakt ist, dass uns die göttliche Formel seit mindestens 2.400 Jahren beschäftigt. Als ältestes bislang anerkanntes Denkmal, das nach dem Goldenen Schnitt geschaffen wurde, gilt der berühmte Parthenon auf der Akropolis in Athen in Griechenland.
Als Erbauer des Tempels gelten die beiden Architekten Iktinos und Kallikrates, die ihr Werk innerhalb von 60 Jahren im Jahr 430 vor Christus beendeten. Ebenfalls beteiligt am Bau des Tempels und seines prächtigen Schmuckes war der griechische Bildhauer Phidias. Mehr als 100 Jahre später schrieb der griechische Mathematiker Euklid die älteste bekannte Definition des Goldenen Schnitts nieder.

Der Parthenon auf der Athener Akropolis, das Wahrzeichen Griechenlands, gilt als ältester Bau, den seine Architekten 430 vor Christus im „göttlichen Verhältnis“ erbauten. Foto: iStock / Epoch Times
Einigen Historikern zufolge könnte der Goldene Schnitt sogar bis zu den Ägyptern zurückreichen. Diese sollen das Verhältnis für heilig gehalten und beim Bau ihrer Tempel und Pyramiden verwendet haben. Vor allem bei dem Bau der berühmten Cheops-Pyramide in Gizeh vor rund 4.500 Jahren soll das goldene Verhältnis angewendet worden sein.
Im Mittelalter wurde der Goldene Schnitt schließlich vermehrt im Bereich der Malerei aufgegriffen und später von Gelehrten wie Kepler und da Pisa. Fortan und bis in die heutige Zeit schufen Architekten immer wieder Meisterwerke mithilfe der Schönheitsformel. Zu den berühmtesten Bauten gehören der Taj Mahal in Indien, das Opernhaus von Sydney (Australien) sowie die Hamburger Elbphilharmonie oder das Alte Rathaus in Leipzig.

Kupferstich vom Alten Rathaus in Leipzig (J. C. Dehne, 1672). Foto: public domain
Erfolgsformel in der Kunst
Die häufigste Anwendung fand die Erfolgsformel mit Abstand in der Kulturepoche der Renaissance. In dieser Zeit des kulturellen Umbruchs rückten die klassischen Werte aus der griechische und römischen Antike wieder in den Mittelpunkt.
Als Meister in der Verwendung des Goldenen Schnitts innerhalb seiner Malereien gilt der italienische Maler Leonardo da Vinci. So sind „Das Abendmahl“ (1494 – 1497) und „Die Dame mit dem Hermelin“ (1486) nur zwei von vielen Beispielen, in denen der Goldene Schnitt vollständig oder annähernd verwendet wurde.

Kein anderer Maler aus der Renaissance verwendete den Goldenen Schnitt häufiger in seinen Kunstwerken als Leonardo da Vinci. „Das Abendmahl“ besitzt gleich viermal das goldene Maß. Foto: public domain / Epoch Times
Auch sein Kunstkollege Raffael verlieh seinen Gemälden „Sixtinische Madonna“ (1514) und „Die Schule von Athen“ (1510) eine göttliche Komposition – ähnlich, wie es bereits Albrecht Dürer mit dem „Selbstbildnis im Pelzrock“ (1500) tat. Bis in die darauffolgenden Jahrhunderte nutzten bekannte Maler wie Caspar David Friedrich („Die Lebensstufen“, um 1835), Claude Monet („Heuhaufen in Giverny“, 1886) und Vincent van Gogh („Frau, im Gras sitzend“, 1887) den Goldenen Schnitt in ihren Malereien. Selbst berühmte Persönlichkeiten wie Johann Wolfgang von Goethe wurden in ihrem Porträt in perfekter Proportion dargestellt.

Auch bei Menschen kann der Goldene Schnitt auftreten. Hier festgehalten in einem Portrait von Johann Wolfgang von Goethe (Stieler 1828, Öl auf Leinwand). Foto: public domain / Epoch Times
Ein kaum bekanntes, aber dennoch weltberühmtes Beispiel für den Goldenen Schnitt schuf der Comic-Zeichner Albert Uderzo. So entwarf der Franzose den beliebten gallischen Hinkelsteinlieferanten Obelix im „göttlichen“ Verhältnis.
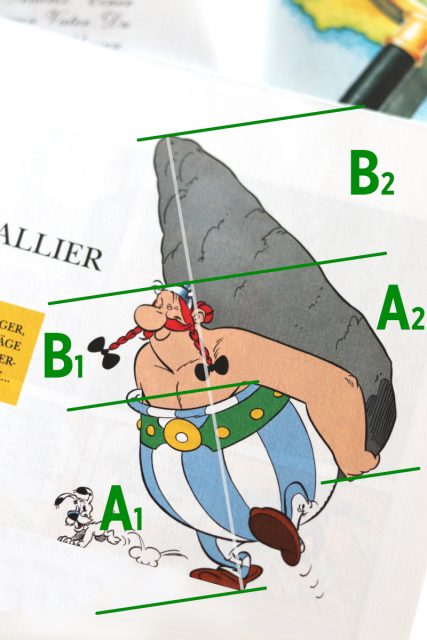
Bei Obelix wendete Albert Uderzo gleich zweimal den Goldenen Schnitt an. Foto: Epoch Times
Auch in der klassischen Musik ist der Goldene Schnitt in vielfältiger Weise zu finden. So kann das goldene Maß auch beim Bau von Musikinstrumenten wie Geigen zum Einsatz kommen. Dabei stellt der Klangkörper die größere Strecke und der Hals zusammen mit der Schnecke die kleinere dar. Weiterhin kann auch ein Musikstück im göttlichen Verhältnis aufgebaut sein. Dabei können zwei Töne oder Teile der Komposition zueinander im Goldenen Schnitt stehen.
Inspiriert von der Natur
Alle Beispiele haben jedoch eines gemeinsam: Der Goldene Schnitt ist ein von der Natur gemachtes Phänomen. So kommt er in Pflanzen bereits bei der Anordnung von Zweigen und Blüten sowie in den Adern der Blätter zum Ausdruck. Als Paradebeispiele gelten neben Rosen, Sonnenblumen und verschiedenen Kohlarten auch Kiefernzapfen oder Agaven. Diese Liste kann problemlos um alle Pflanzen erweitert werden, die eine fünfzählige Symmetrie aufweisen.

Mit Abstand am häufigsten ist der Goldene Schnitt in der Pflanzenwelt zu finden. Ihr Erfinder? Die Natur selbst. Foto: iStock / Epoch Times
Entsprechende Vergleiche finden sich mit Seesternen, Schnecken, Pferden oder Bienen auch in der Tierwelt.

Tierisch gut: Die Natur schuf auch Pferde und Bienen nach dem göttlichen Verhältnis. Foto: iStock / Epoch Times
Sogar in der Geometrie von Kristallen, bei Wetterereignissen wie Wirbelstürmen oder in den Weiten des Weltalls kommt sie zum Ausdruck.

Die ästhetische „goldene“ Spiralform tritt sogar bei Wirbelstürmen und im Universum auf. Foto: iStock, NASA / Epoch Times
Aufgrund der einzigartigen Eigenschaften dieser goldenen Proportion betrachten sie viele Menschen als heilig oder göttlich. Es enthüllt uns das Tor zu einem tieferen Verständnis von Schönheit und einer verborgenen Harmonie in so vielem, was wir täglich sehen.



























vielen Dank, dass Sie unseren Kommentar-Bereich nutzen.
Bitte verzichten Sie auf Unterstellungen, Schimpfworte, aggressive Formulierungen und Werbe-Links. Solche Kommentare werden wir nicht veröffentlichen. Dies umfasst ebenso abschweifende Kommentare, die keinen konkreten Bezug zum jeweiligen Artikel haben. Viele Kommentare waren bisher schon anregend und auf die Themen bezogen. Wir bitten Sie um eine Qualität, die den Artikeln entspricht, so haben wir alle etwas davon.
Da wir die Verantwortung für jeden veröffentlichten Kommentar tragen, geben wir Kommentare erst nach einer Prüfung frei. Je nach Aufkommen kann es deswegen zu zeitlichen Verzögerungen kommen.
Ihre Epoch Times - Redaktion