
Finden Sie beide Rätsel-Lösungen? – Angeblich braucht man dafür ein IQ von 130+

Mathematik ist einfach. Entweder ist eine Aufgabe richtig oder falsch, oder? Im Prinzip ja, aber … Denn obwohl dieses Rätsel auf den ersten Blick nach dem Lösungsblatt eines schlechten Schülers aussieht, versteckt sich mehr dahinter.
Nun könnten Skeptiker sagen: „Die Antwort lautet 19“ – und haben damit vollkommen recht. Es macht keinen Unterschied, dass zwei der vorherigen Gleichungen falsch sind. Wenn Sie 19 zu Ihrer finalen Antwort erklären, kann niemand widersprechen. Das ist ein unkonventioneller Gedanke!
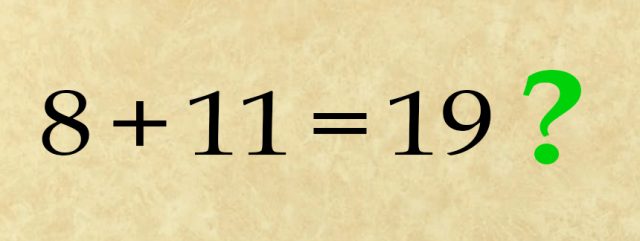
Mathematisch korrekt ist lediglich die Lösung 19. Andernfalls verlangt das Rätsel eine etwas freiere Auslegung der Aufgabe. Foto: Epoch Times
Für diejenigen, die ihre mathematischen Fähigkeiten ein bisschen mehr fordern wollen, hält dieses Rätsel jedoch noch ein paar Überraschungen bereit. Angeblich sollen nur hochbegabte Menschen mit einem IQ von über 130 beide Lösungen finden können.
Es gibt ein paar verborgene Muster in der Abfolge der Gleichungen, die alles miteinander verbinden. Wer diese Muster findet, kann beide Lösungen – neben der mathematisch korrekten Antwort 19 – berechnen.
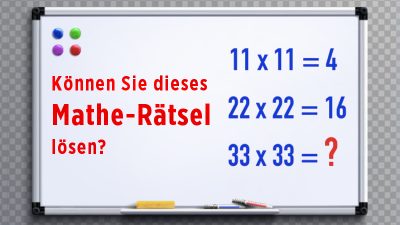
Rätsel mit Trick – Finden Sie beide Lösungen?
Nehmen Sie sich einen Moment Zeit, um zu überlegen, welche Muster am Werk sind und versuchen Sie, sich beide Lösungen auszudenken, bevor Sie nach unten scrollen, um die Antworten unten zu sehen.
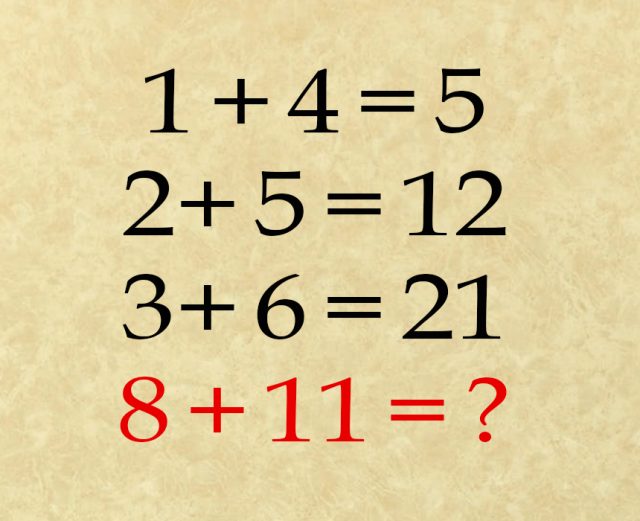
Versuchen Sie beide Lösungen zu finden, bevor Sie nach weiter lesen. Foto: Epoch Times
Die erste Gleichung ist natürlich richtig und logisch: 1 + 4 = 5. Aber da scheint die Logik zu enden. Die zweite und dritte Gleichung, 2 + 5 = 12 und 3 + 6 = 21, sind mathematischer Blödsinn. Links und rechts des Gleichungszeichens steht nicht derselbe Wert.
Erst das Vorhandensein eines größeren Musters oder einer versteckten Regel macht die Aufgabe sinnvoll. Erst wenn wir diese bestimmen können, lässt sich die letzte Gleichung vielleicht lösen.
Das Muster
Natürlich gibt es ein verstecktes Muster. Fügen Sie zur linken Seite einer beliebigen Gleichung die Antwort der vorherigen Gleichung hinzu. Im Falle der ersten Gleichung gibt es keine vorherige Gleichung, und so würden Sie auf der linken Seite der Gleichung eine Null hinzufügen (0 + 1 + 4). Am Ergebnis ändert sich deshalb aber noch nichts.
Dasselbe Muster funktioniert jedoch auch für die zweite und dritte Gleichung und siehe da, Aufgabe und Lösung passen plötzlich zusammen. Wer mit diesem Wissen die letzte Gleichung betrachtet, findet schnell eine Lösung.
Durch Addition des Ergebnisses der dritten Gleichung zur linken Seite der vierten Gleichung ergibt sich 21 + 8 +11. Daraus ergibt sich die erste Lösung 40. Doch das ist noch nicht alles.
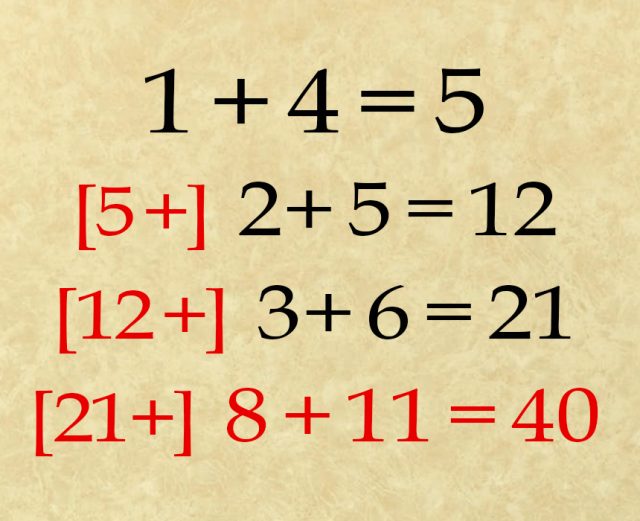
Die Addition der Ergebnisse über Zeilen hinweg erlaubt das Rätsel zu lösen. Foto: Epoch Times
Man könnte denken, dass 40 die finale Lösung ist, aber in Wirklichkeit versteckt sich in diesem Rätsel noch ein anderes Muster. Es basiert auf dem Ersten, führt aber zu einer anderen, ebenfalls logischen Antwort.
Fehlt da nicht noch was?
Statt Zeile für Zeile zu betrachten, verlangt die zweite Lösung einen Blick auf die Spalten. Die erste Zahl aus jeder der drei Gleichungen erzeugt eine aufsteigende Reihe: 1, 2, 3. Fast selbstverständlich formen auch die zweiten Zahlen der ersten drei Gleichungen eine lückenlose Zahlenfolge: 4, 5, 6.
Nur die letzte Gleichung scheint mit diesen Reihen zu brechen. Scheinbar, denn der Abstand zwischen der ersten und zweiten Zahl ist identisch. In der Tat passt auch diese Zeile in das größere Muster – wenn man sich eingesteht, dass weitere Zeilen zwar existieren, aber aus dem Blickfeld verschwunden sind.
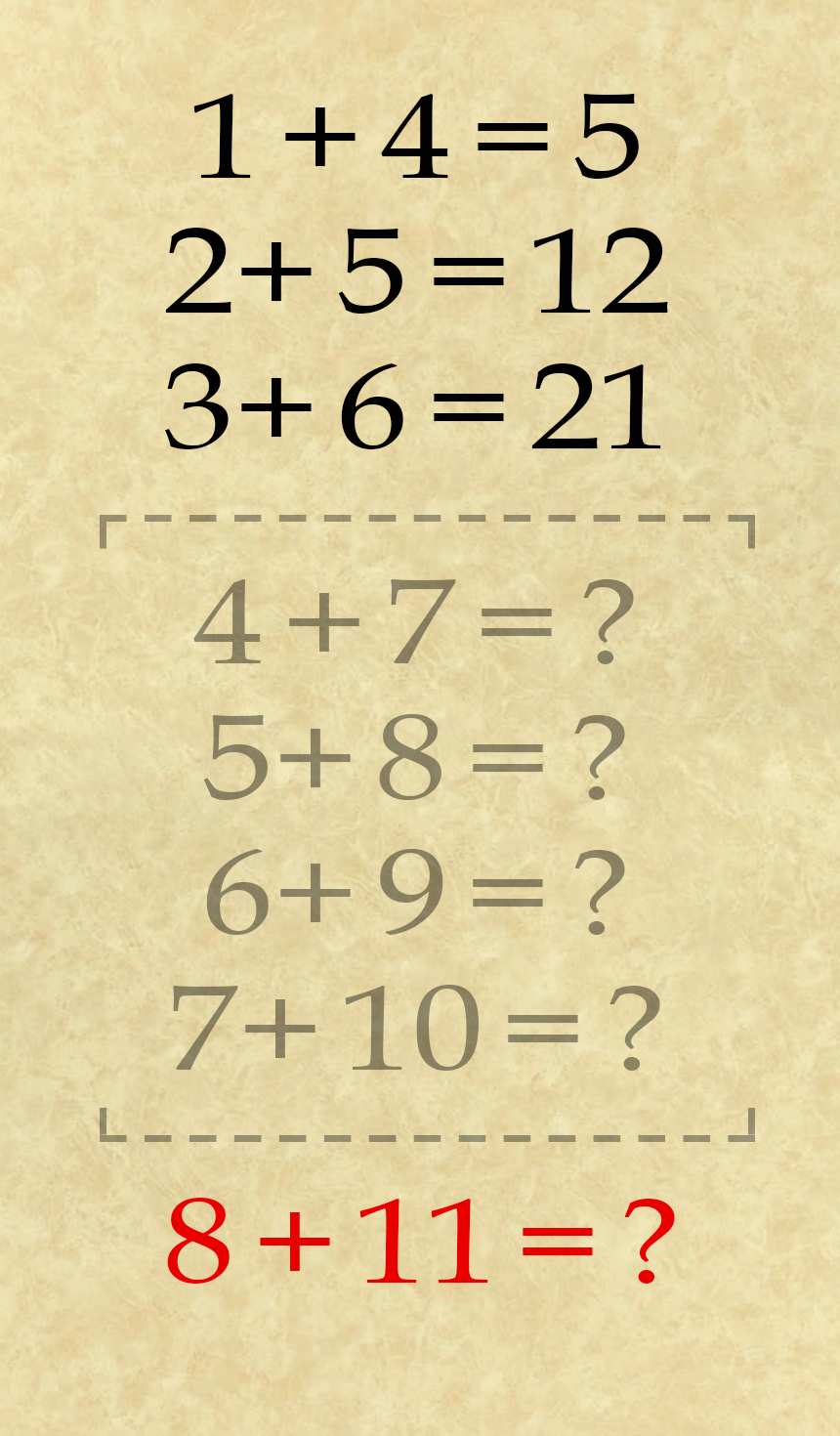
Das Rätsel versteckt noch mehr. Die gegebenen Gleichungen implizieren das Vorhandensein vier weiterer Zeilen. Foto: Epoch Times
Durch die Ergänzung weiterer Zeilen kann das finale Ergebnis natürlich nicht mehr 40 lauten. Angenommen, man verwendet dieselbe Regel wie bei der ersten Lösung für die verbleibenden Zeilen – einschließlich der letzten Zeile – erhält man eine andere Antwort.
Nach allen neu eingefügten Gleichungen beträgt das Zwischenergebnis in der vorletzten Zeile 77. Daraus ergibt sich für die letzte Zeile schließlich 77 + 8 + 11 und das addiert sich zu 96.
Dürfen Sie sich als hochbegabt bezeichnen? Haben Sie beide Lösungen gefunden?

Die vier zusätzlichen Rätsel-Zeilen berechnen sich nach derselben Methode und erhöhen das endgültige Ergebnis auf 96. Foto: Epoch Times
Bonus für Mathe- und Rätsel-Geeks
In der Mathematik gibt es für das fortschreitende Aufsummieren von Zahlen eine eigenen Term: die Summe ∑. Auch in diesem konkreten Rätsel können die Gleichungen in einem Summenausdruck zusammengefasst werden. Der konstante Abstand der beiden Summanden in jeder Zeile erleichtert dies zusätzlich.
Statt 1 + 4 = 5 hätte man auch X1 + (X1 + 3) = 5 oder 2 X1 + 3 = 5 schreiben können, wobei X1 = 1 ist und die Nummer der Zeile widerspiegelt. Die linke Seite der zweiten Zeile lautet ohne Ergänzung des Ergebnisses aus der ersten Gleichung: 2 + 5 oder (X1 + 1) + (X1 + 1) + 3 oder 2 (X1 + 1) +3.
Für das Ergebnis der ersten Gleichung kann man ebenfalls einen Term mit X einsetzen. Daraus folgt [2 X1 + 3] + [2 (X1 + 1) + 3] und mit X1 = 1 das Ergebnis 12. Dabei gilt X1 + 1 = X2 oder allgemein X(n+1) = Xn + 1.
Mit jeder weiteren Zeile kommt ein weiterer Summand hinzu, dessen X-Wert um eins steigt. Diese Reihe könnte man unendlich fortschreiben – oder in einem Summenausdruck zusammenfassen:
Setzt man nun für n – n steht für die n-te Zeile der Aufgabe – eine beliege Zahl ein, erhält man ohne Umschweife das Ergebnis dieser Zeile.
Wer diese Formel auf Grundlage der ersten drei Zeilen erstellen kann und n = 8 einsetzt, erhält auch in der ersten Version schon das Ergebnis 96. Die Summe ergänzt die fehlenden Zeilen automatisch.
Und nur so nebenbei, das Ergebnis der 42. Zeile lautet 1932 …



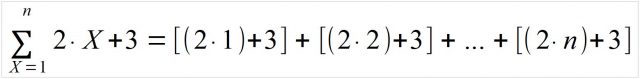




























vielen Dank, dass Sie unseren Kommentar-Bereich nutzen.
Bitte verzichten Sie auf Unterstellungen, Schimpfworte, aggressive Formulierungen und Werbe-Links. Solche Kommentare werden wir nicht veröffentlichen. Dies umfasst ebenso abschweifende Kommentare, die keinen konkreten Bezug zum jeweiligen Artikel haben. Viele Kommentare waren bisher schon anregend und auf die Themen bezogen. Wir bitten Sie um eine Qualität, die den Artikeln entspricht, so haben wir alle etwas davon.
Da wir die Verantwortung für jeden veröffentlichten Kommentar tragen, geben wir Kommentare erst nach einer Prüfung frei. Je nach Aufkommen kann es deswegen zu zeitlichen Verzögerungen kommen.
Ihre Epoch Times - Redaktion